Переработка иловых осадков сточных вод и шлама
Центр переработки осадков сточных вод и шламов
RusEcoTech llc.

Объем переработки в 10 000 000 куб. метров
Вы сможете переработать объем осадка сточных вод, начиная от 20 000 до 10 000 000 кубометров. При цикле переработки в 60 дней.

Старт переработки в течение 7 дней
Благодаря реагентному методу переработки иловых осадков сточных вод Вы освобождаетесь от необходимости строительства дополнительных сооружений на территории карты и экономите время. Все работы происходят на месте (на иловой карте).

Уменьшение расходов на 300% в альтернативе со сжиганием осадка
Вы уменьшите свои расходы на переработку в 4 раза (на 300%) по сравнению с методами фильтрования, прессования и сжигания иловых осадков сточных вод.

Конечный продукт - органо-минеральная композиция
Вы обеззаразите и обезопасите конечный продукт переработки. В итоге на выходе процесса получается готовая для использования в соответствии санитарным нормам минеральная композиция (грунт).
Реагентная технология переработки ОСВ может помочь Водоканалам, промышленным предприятиям и муниципальным органам
Потому что накопление иловых осадков сточных вод ведет к:
- Гибели окружающей флоры и фауны.
- Загрязнению почвы, рек, водоемов и грунтовых вод тяжелыми металлами.
- Эпидемиологической опасность от паразитов и гельминтов.
- Распространению фекального запаха.
При этом:
- Ужесточается государственный контроль их переработки.
- Увеличиваются штрафы.
- Существующие методы утилизации ведут к их накоплению.
- Альтернативные методы переработки осадков сточных вод (сжигание, геотубирование и захоронение на полигоне) приводят не к их переработке, а трансформации в другие виды отходов.
- Отсутствует возможность сокращения охранных зон.
Но Вы сможете улучшить экологическую обстановку при снижении расходов на переработку
Решение Вашей проблемы – это производство продукции (органо-минеральной композиции грунта).
Применение нашей технологии на любой стадии образования осадков обеспечивает безотходность производственного цикла очистки сточной воды. А так же получение продукции, которую можно использовать для строительства дорог, удобрения почвы и прочих хозяйственных работ.
Кроме этого при переработке осадков сточных вод произойдёт:
- Подавление патогенной микрофлоры и кишечной палочки.
- Уничтожение жизнеспособных яиц гельминтов и сальмонелл.
- Изменение структуры осадка, которое способствует развитию почвенной микрофлоры, повышает гумусность, влагоудержание, а так же эрозийную устойчивость будущей почвы.
Вы можете получить бесплатный расчет стоимости переработки осадка сточных вод для вашего индивидуального проекта
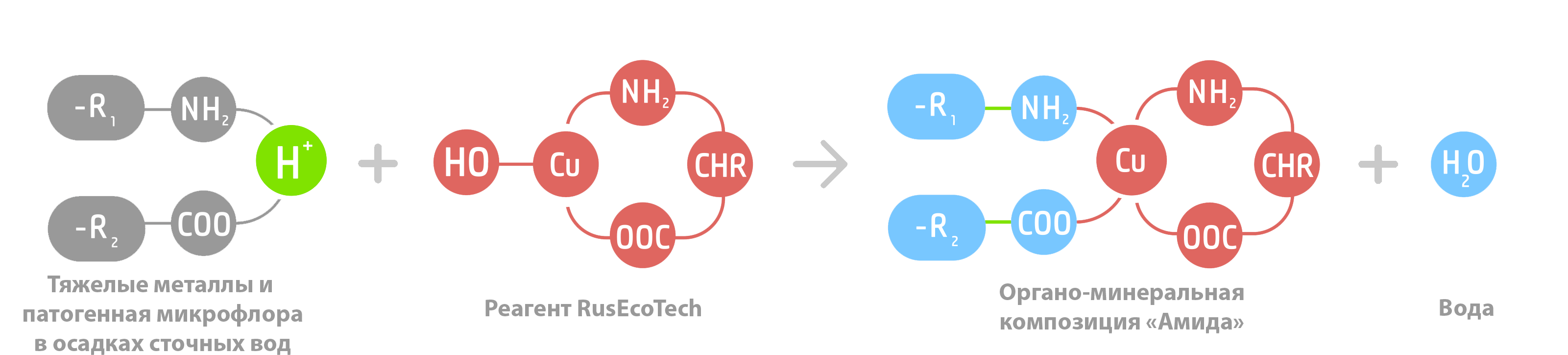
Как работает технология RusEcoTech?
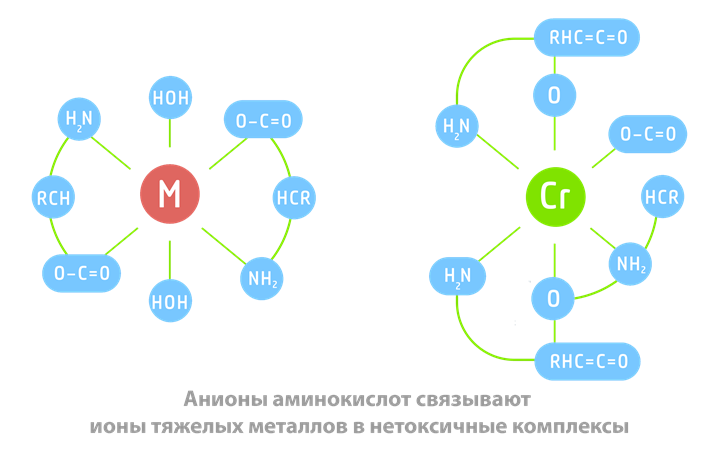
Это приводит к детоксикации тяжелых металлов солями аминокислот
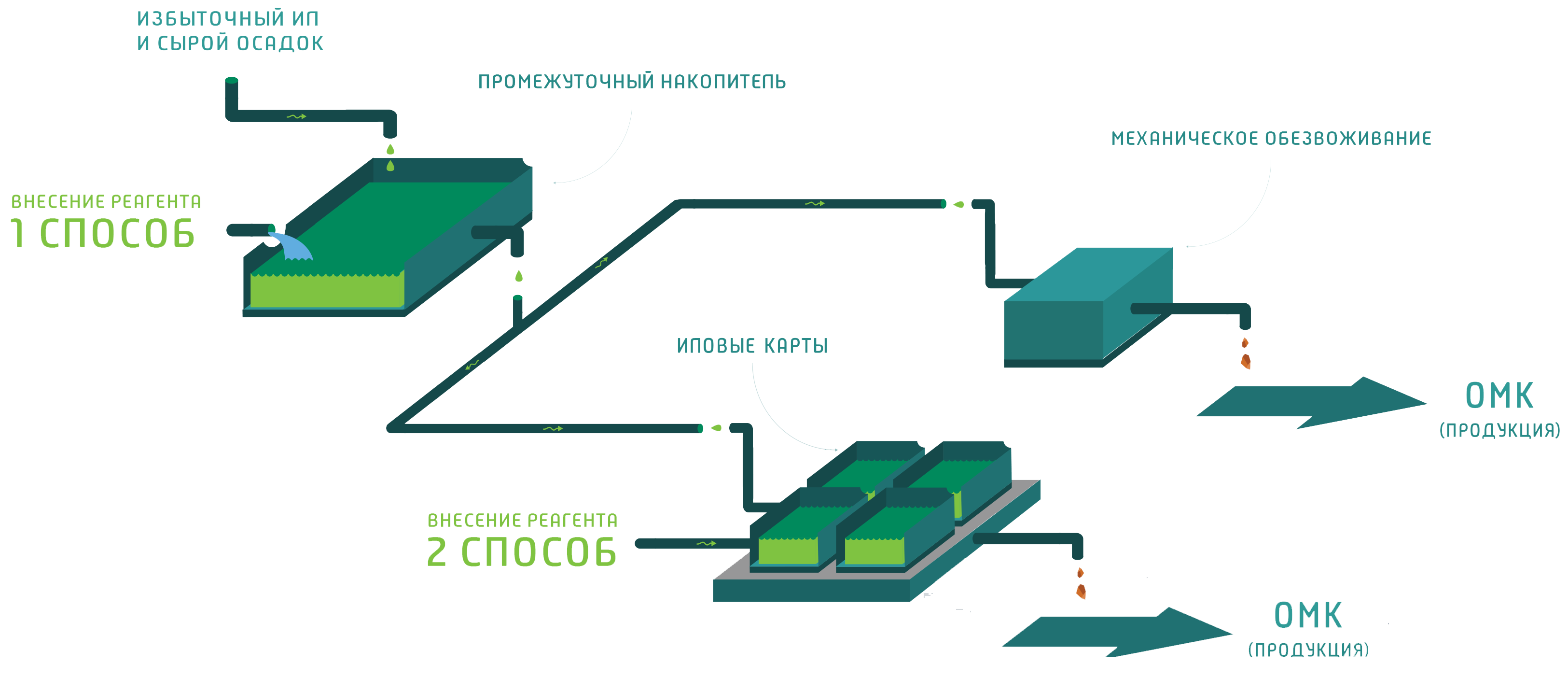
Возможно применять на любой стадий обработки осадка сточных вод
В результате Вы получите
Комплексную услугу по переработке и результат:
- Органо-минеральная композиция «АМИДА», представляющую собой техногенный грунт, без фекального запаха.
- Свободный площади на иловых картах.
- Улучшение экологической обстановки.
- Время полной переработки 60 дней (в зимнее время и 30 дней в другой сезон).
- 75% сэкономленных денежных средств по сравнению с альтернативными методами переработки (геотубированием, сжиганием и захоронением на полигонах).
Закажите бесплатный расчет переработки осадков сточных вод на Вашем объекте.
И для этого оставьте нам свои контактные данные, чтобы наши специалисты связались с Вами для уточнения ряда деталей.
Процесс работ Вы можете посмотреть в видео:
При полном контроле процесса переработки
Процесс переработки проводится под 100% контролем специалистов ООО «РусЭкоТех».
Вы получите готовый результат:
- Экологический мониторинг местности.
- Исследовательские работы осадка сточных вод.
- Расчет количества реагента и методов его применения.
- Переработка осадка сточных вод в минеральную композицию (грунт).
- Механизированные работы по вывозу готового продукта переработки (при необходимости).
- Регулярный контроль процесса переработки.
- Документальное сопровождение.